Как насекомые создают силы, необходимые для полетаСтраница 1
Введение.
Кто из нас не любовался бесшумным полетом бабочек на залитой солнцем лужайке или стремительными бросками мухи – журчалки над цветущей геранью? Кто не замирал от удивления, следя за виртуозными движениями стрекоз, гоняющихся друг за другом вдоль берега? Все мы отдаем должное полетному мастерству этих крохотных существ. Но самое поразительное состоит в том, что насекомые научились летать очень давно – не менее трети миллиарда лет прошло с тех пор, как насекомые порхают и носятся над поверхностью Земли. А наши знания о том, как работает крыловой аппарат, до сих пор поверхностны.
Ключевым вопросом в изучении полета насекомых остается проблема создания аэродинамических сил в машущем полете. Выяснить природу этих сил пытались еще первые исследователи полета насекомых. Немецкий исследователь Е.Хольст в 1943 году первым экспериментально доказал, что господствовавшие ранее представления о полете насекомых как о гребном не соответствуют принципу работы машущего крыла. На смену упрощенным и неточным представлениям об отбрасывании воздуха пришел так называемый квазистационарный подход, при котором аэродинамические процессы сводились к теории стационарных состояний, поддающихся расчету методами классической аэродинамики. Исследование полета саранчи в Лондонском противосаранчовом центре (The Antilocust Research Centre), в 1956 году показало высокое совпадение расчетных данных с реально измеренными средними значениями аэродинамических сил. Несмотря на общепризнанность квазистационарного подхода, никому больше не удавалось добиться соответствия расчетных значений сил реальным, что заставляет предполагать наличие дополнительных аэродинамических сил. Кроме того, многие авторы отмечают нестационарный характер создаваемых в полете сил и необычное поведение воздушных струй за летящим насекомым.
Физические основы полета.
Локомоция в сплошных средах (воздухе и воде) настолько отличается от передвижения на границе раздела сред, что заслуживает особого внимания природа сил, делающих такое движение возможным. Сплошная среда представляет собой континуум, в котором не на что опереться, не от чего оттолкнуться. В вязкой жидкости, каковой является вода и воздух, возможны две основные формы движения: ламинарное, или слоистое, когда линии тока параллельны друг другу, и турбулентное, при котором происходит перемешивание жидкости. В турбулентных течениях скорость и давление в каждой точке пространства непостоянны и характеризуются нерегулярными высокочастотными пульсациями.
Всякое тело, движущееся в сплошной среде, испытывает на своей поверхности нормальные и касательные напряжения. Их результирующая представляет собой силу полного сопротивления среды движению тела, причем вектор силы полного сопротивления далеко не всегда совпадает с направлением движения. Проекция полного сопротивления тела на ось х в скоростной системе координат (ось х направлена вдоль скорости движения, ось z перпендикулярна к ней в горизонтальной плоскости, а ось у - в вертикальной) есть лобовое сопротивление, проекция же на ось у при положительном у есть подъемная сила, при отрицательном – в зависимости от того, где происходит движение, либо топящая (в воде), либо отрицательная подъемная сила (в воздухе). Лобовое сопротивление складывается из сопротивления трения и сопротивления давления или сопротивления формы (разности давлений впереди и позади тела). Количественно лобовое сопротивление и подъемная сила выражаются формулами:
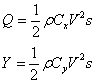
где S – некоторая характерная площадь тела, V - скорость движения, r- плотность среды, сх и су – безразмерные коэффициенты соответственно лобового сопротивления и подъемной силы. Они зависят от формы движущегося тела, его ориентации в пространстве, но, прежде всего от соотношения сил инерции (они проявляются в давлении на поверхность тела) и трения, которые определяются вязкостью. Соотношение этих сил дает безразмерный комплекс, численное значение которого должно быть одинаковым у подобных течений. Иными словами, речь идет о масштабном критерии, который дает возможность сравнивать движение различных объектов, имеющих разные характеристики. Этот комплекс получил название числа Рейнольдса (Re):